Cách chứng minh 4 điểm cùng thuộc một đường tròn cực dễ hiểu

Đường tròn là một nội dung kiến thức quan trọng trong chương trình môn Toán lớp 9. Vậy, đường tròn được xác định khi nào? Và khi cho 4 điểm bất kì thì làm sao để nhận biết 4 điểm đó có cùng thuộc một đường tròn hay không? Để hiểu rõ hơn cách chứng minh 4 điểm cùng thuộc một đường tròn, chúng ta hãy cùng tìm hiểu bài viết sau đây.

1. Nhắc lại một số kiến thức

• Đường tròn được xác định khi biết tâm và bán kính
• Đường tròn được xác định khi biết một đoạn thẳng là đường kính của đường tròn. Trong trường hợp này, tâm của đường tròn chính là trung điểm của đường kính, còn bán kính có độ dài bằng đường kính chia 2
• Đường tròn có tâm là O, bán kính là R được kí hiệu là (O; R)
• Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn. Hay nói cách khác, điều kiện để ba điểm cùng thuộc một đường tròn là ba điểm đó không thẳng hàng

Khi cho ba điểm không thẳng hàng, ta luôn vẽ được một tam giác. Đường tròn đi qua ba đỉnh của tam giác có tâm là giao điểm của các đường trung trực trên các cạnh của tam giác, bán kính có độ dài từ tâm tới một đỉnh của tam giác. Lúc này, tam giác được gọi là nội tiếp đường tròn hay đường tròn ngoại tiếp tam giác

2. Các cách chứng minh 4 điểm cùng thuộc một đường tròn

2.1. Chứng minh 4 điểm cùng thuộc một đường tròn bằng cách chỉ ra có 1 điểm nào đó cách đều 4 điểm đã cho

Ví dụ: Cho hình bình hành ABCD. Từ A kẻ AH DC (H DC), từ C kẻ CK AB (K AB). Chứng minh 4 điểm A, H, C, K cùng thuộc một đường tròn

Giải

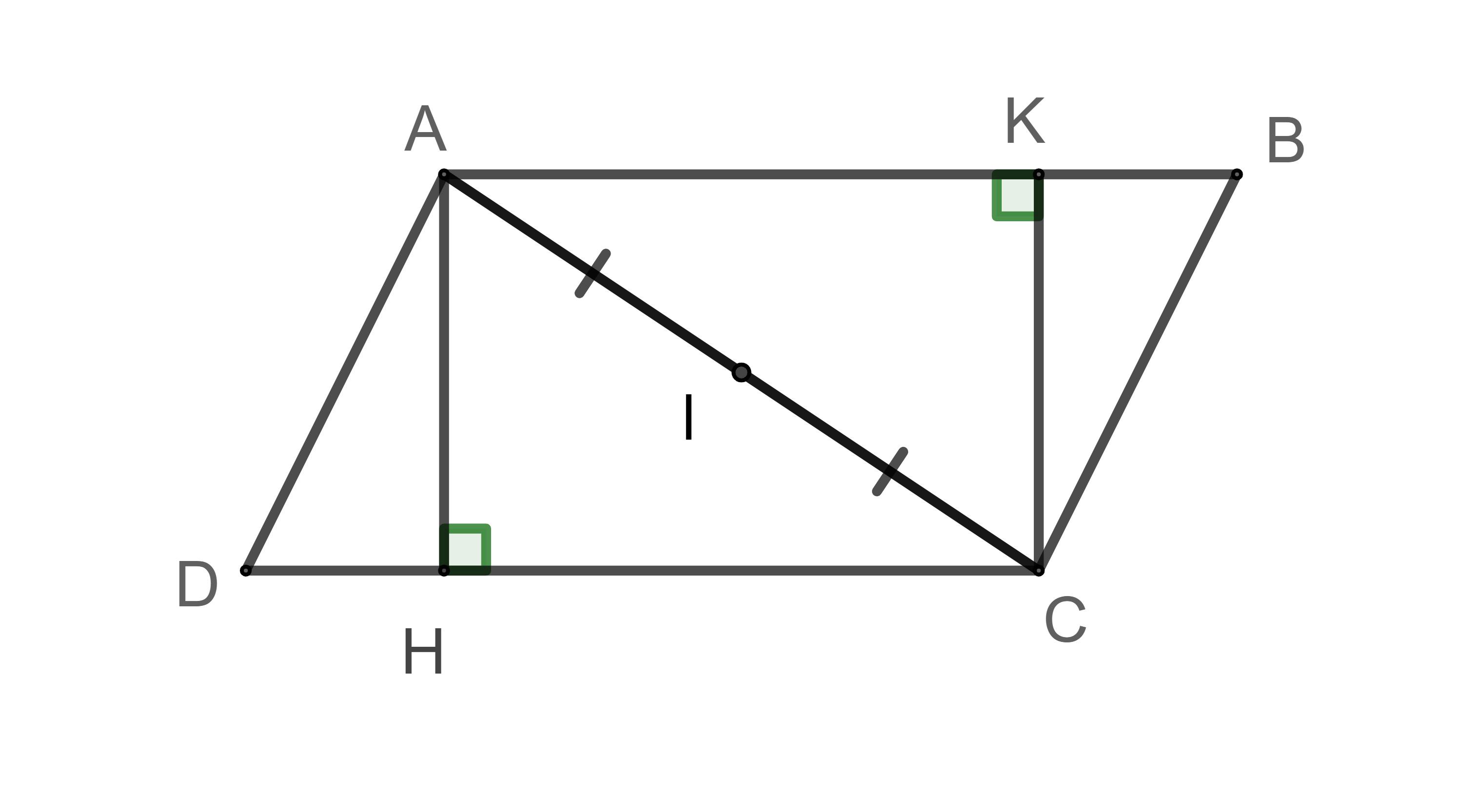
Gọi I là trung điểm của AC

AHC vuông tại H có HI là đường trung tuyến ứng với cạnh huyền nên HI = IA = IC (1)

AKC vuông tại K có KI là đường trung tuyến ứng với cạnh huyền nên KI = IA = IC (2)

Từ (1) và (2) ta có: IH = IK = IA = IC

Suy ra 4 điểm A, H, C, K đều cách đều I

Vậy, 4 điểm A, H, C, K cùng thuộc một đường tròn

2.2. Chứng minh 4 điểm cùng thuộc một đường tròn bằng cách chỉ ra có hai góc kề bằng nhau cùng nhìn một cạnh

Ví dụ: Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm N sao cho AN = AB, trên tia đối của tia AB lấy điểm M sao cho AM = AC. Chứng minh 4 điểm B, C, M, N cùng thuộc một đường tròn

Giải

• Xét tam giác AMN và tam giác ACB có:

= = 900 (gt)

AM = AC (gt)

AN = AB (gt)

( 2 cạnh góc vuông)

MN = CB ( 2 cạnh tương ứng)

• Ta có: NC = NA + AC và BM = BA + AM

Mà NA = BA (gt) và AC = AM (gt)

NC = BM

• Xét tam giác MNC và tam giác CBM có:

MN = CB (cmt)

NC = BM (cmt)

MC là cạnh chung

(c.c.c)

( 2 góc tương ứng)

Mà hai góc này cùng nhìn cạnh MC

Vậy, 4 điểm B, C, M, N cùng thuộc một đường tròn

2.3. Chứng minh 4 điểm cùng thuộc một đường tròn bằng cách chỉ ra trong tứ giác tổng hai góc đối diện bằng 1800

Ví dụ: Cho tứ giác ABCD có = 800; = 1200; = 1000; = 600. Hỏi 4 điểm A, B, C, D có cùng thuộc một đường tròn hay không? Tại sao?

Giải

Trong tứ giác ABCD có và là hai góc đối nhau

Mà + = 800 + 1000 = 1800

Vây, 4 điểm A, B, C, D cùng thuộc một đường tròn

Chú ý: Từ 4 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng ta vẽ được một tứ giác. Nên khi 4 điểm cùng thuộc một đường tròn ta cũng có thể nói tứ giác nội tiếp đường tròn hay đường tròn ngoại tiếp tứ giác.

3. Bài tập áp dụng cách chứng minh 4 điểm cùng thuộc một đường tròn

Bài 1: Cho tứ giác ABCD nội tiếp (O; R). Biết = 600; = 1100. Khi đó số đo và lần lượt là

1. 1200; 700
2. 700; 1200
3. 800; 1000
4. 1000; 800

Hướng dẫn: Vì tứ giác ABCD nội tiếp (O; R) nên

• + = 1800

= 1800 - = 1800 - 600 = 1200

• + = 1800

= 1800 - = 1800 - 1100 = 700

Vậy, = 1200; = 700

Chọn câu A

Bài 2: Cho hình vuông ABCD. Gọi I là giao điểm hai đường chéo AC, BD. Trong các phát biểu dưới đây, phát biểu đúng là

1. 4 điểm A, B, C, D cùng thuộc đường tròn tâm I, bán kính AC
2. 4 điểm A, B, C, D cùng thuộc đường tròn tâm I, bán kính BD
3. 4 điểm A, B, C, D cùng thuộc đường tròn tâm I, bán kính IA
4. 4 điểm A, B, C, D cùng thuộc đường tròn tâm I, đường kính IA

Hướng dẫn: Trong hình vuông, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường

Nên IA = IB = IC = ID

Vậy, 4 điểm A, B, C, D cùng thuộc đường tròn tâm I, bán kính IA

Chọn câu C

Bài 3: Hình có 4 điểm cùng thuộc một đường tròn là

1. Hình bình hành
2. Hình thoi
3. Hình thang
4. Hình thang cân

Hướng dẫn: Vẽ hình thang cân ABCD (AB//CD) có hai đường chéo là AC, BD

Xét tam giác ADC và tam giác BCD có:

AD = BC ( 2 cạnh bên của hình thang cân)

AC = BD ( 2 đường chéo của hình thang cân)

CD là cạnh chung

(c.c.c)

( 2 góc tương ứng)

Mà hai góc này cùng nhìn cạnh CD

Vậy A, B, C, D cùng thuộc một đường tròn

Chọn câu D

Bài 4: Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm AC, BC. Trên tia đối của tia NM lấy điểm K sao cho NK = NM. Trong các phát biểu dưới đây, phát biểu sai là

1. Tứ giác AMKB là hình chữ nhật
2. 4 điểm A, M, K, B cùng thuộc một đường tròn
3. MK = 2.MN
4. 4 điểm B, M, C, K cùng thuộc một đường tròn

Hướng dẫn:

• Vì K là điểm thuộc tia đối NM nên N, M, K thẳng hàng

Mà NK = NM nên NK + NM = MK = 2.MN

Vậy, câu C đúng

• Vì M, N lần lượt là trung điểm AC, BC nên MN là đường trung bình của ABC

MN // AB và MN = .AB

MK // AB và MK = 2.MN = AB

Tứ giác AMKB là hình bình hành

Mà = 900 (gt)

Tứ giác AMKB là hình chữ nhật

Vậy, câu A đúng

• Do AMKB là hình chữ nhật (cmt) nên + = 900 + 900 = 1800

Mà đây là hai góc đối nhau nên 4 điểm A, M, K, B cùng thuộc một đường tròn

Vậy, câu B đúng

Chọn câu D

Bài 5: Trong các hình sau: hình thoi, hình bình hành, hình thang, hình vuông, hình chữ nhật, hình thang cân. Tứ giác có có 4 đỉnh nằm trên đường tròn có tâm là giao điểm hai đường chéo là

1. Hình thoi, hình thang cân
2. Hình vuông, hình chữ nhật
3. Hình vuông, hình bình hành
4. Hình vuông, hình thang

Chọn câu B

Trên đây là một số cách chứng minh 4 điểm cùng thuộc một đường tròn và các bài tập liên quan. Mong rằng các em có thể vận dụng để làm nhiều bài tập hơn nữa và đạt kết quả cao trong các kì thi sắp tới.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang